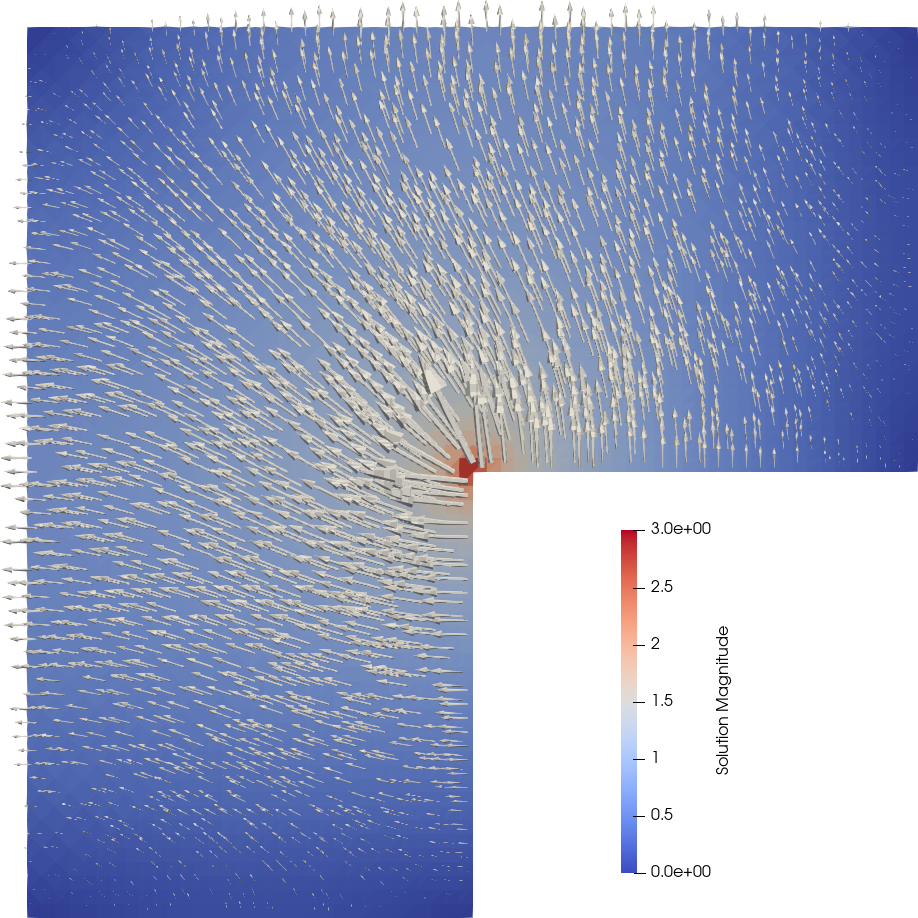
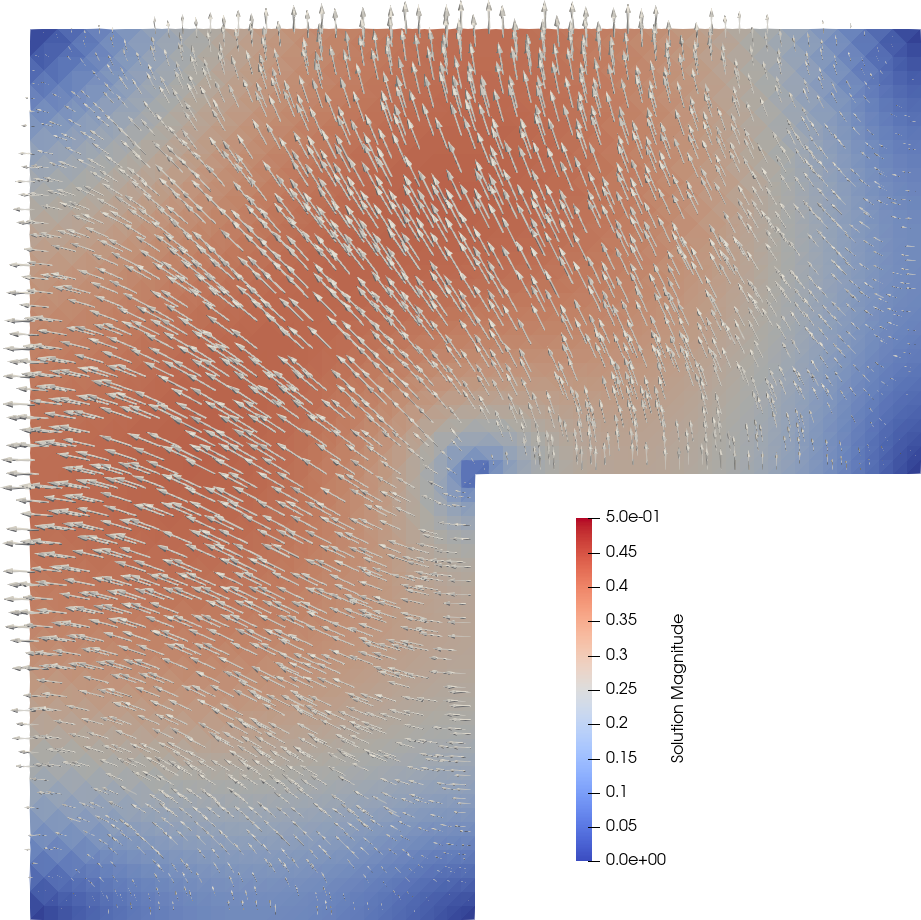
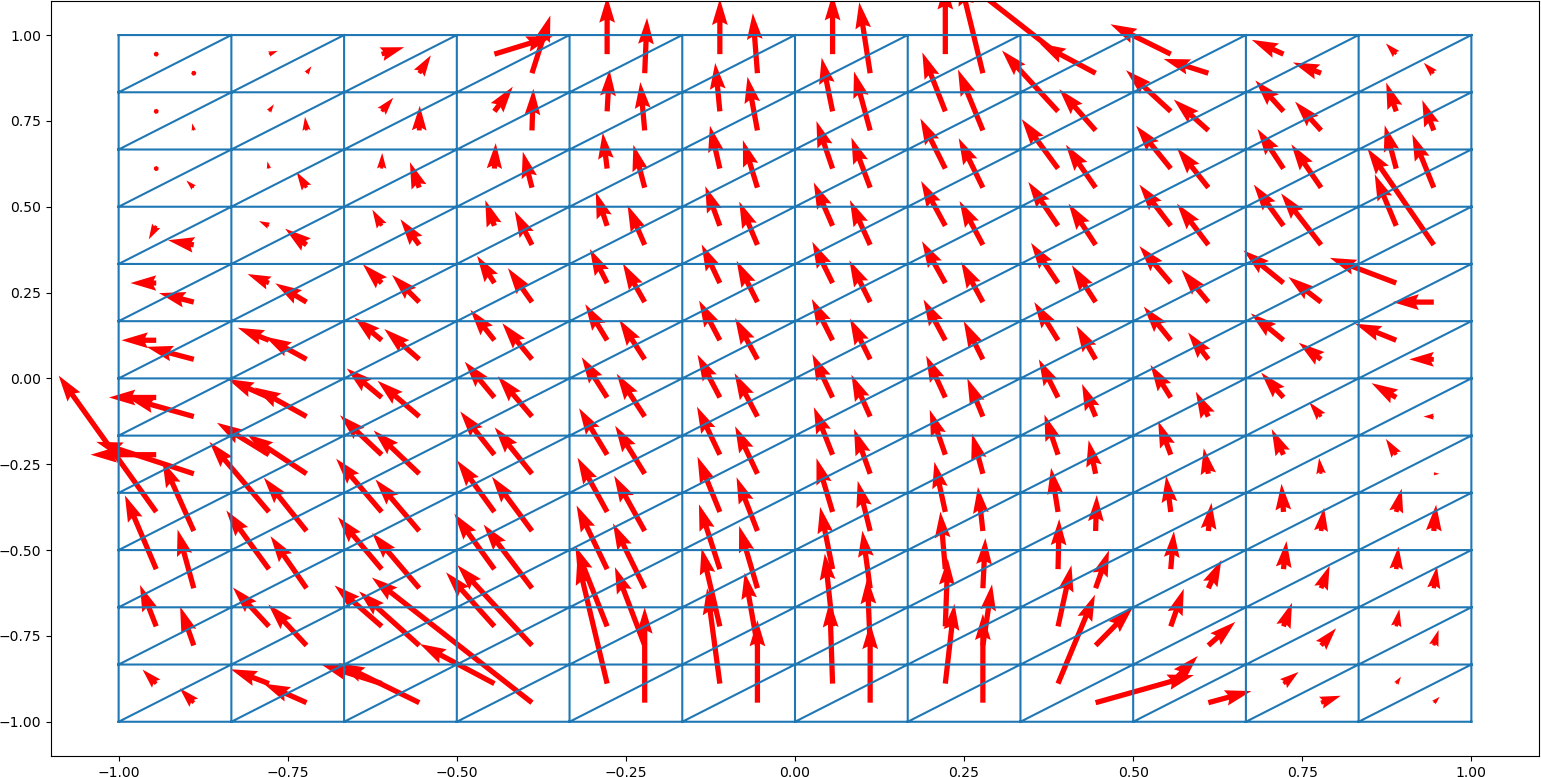
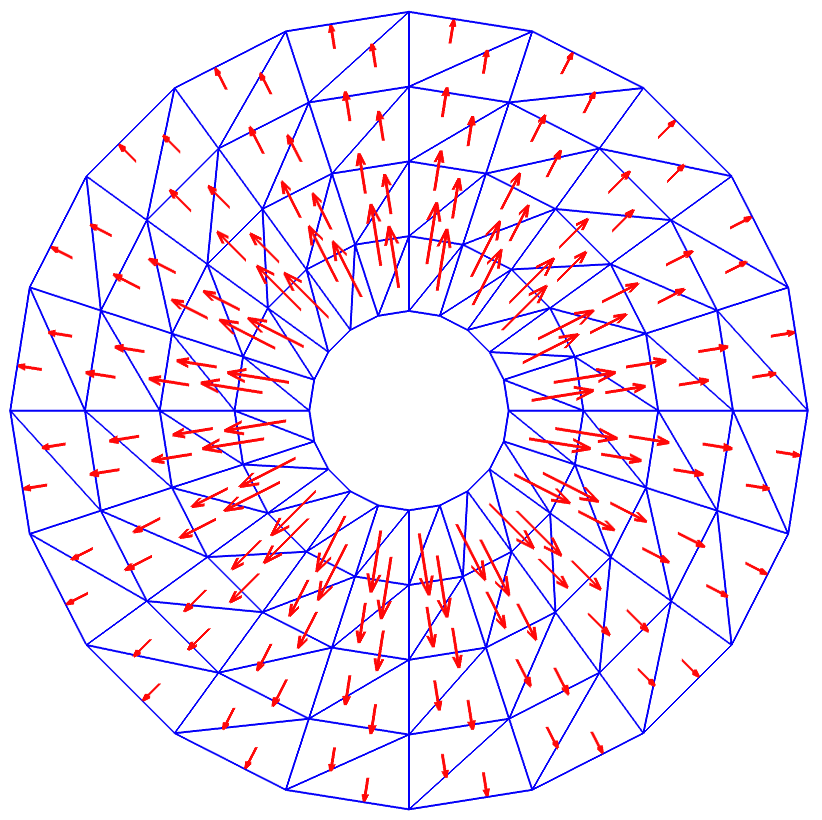
|
Since 09/2021
|
Bernoulli Instructor, EPFL, Switzerland.
|
|
01/2021 - 06/2021
|
Postdoctoral Scholar, UC San Diego, USA.
|
|
09/2020 - 12/2020
|
Postdoctoral Scholar, ICERM, Brown University, Providence, USA
Program Advances in Computational Relativity
|
|
07/2019 - 12/2019
|
Visitor at Isaac Newton Institute, University of Cambridge, UK.
Program Geometry, compatibility and structure preservation in computational differential equations
|
|
07/2017 - 06/2020
|
S.E.W Visiting Assistant Professor, UC San Diego, USA.
|
|
09/2015 - 05/2016
|
Visiting Research Scholar, University of Minnesota.
|
|
06/2010 - 09/2010
|
Visiting Scholar, Jülich Supercomputing Centre.
Domain Distribution for parallel Modeling of Root Water Uptake.
Proceedings 2010, JSC Guest Student Programme on Scientific Computing, 2010.
[Link]
|